Panjebar Semangat
Makalah iki nyinaoni aplikasi pendekatan heuristik sing beda kanggo masalah tata letak fasilitas nyata ing perusahaan manufaktur mebel. Kabeh model dibandhingake nggunakake AHP, ngendi sawetara paramèter kapentingan dipunginaaken. Eksperimen kasebut nuduhake manawa pendekatan modeling tata letak formal bisa digunakake kanthi efektif kanggo masalah nyata sing diadhepi ing industri, sing nyebabake perbaikan sing signifikan.
1. PURWAKA
Industri furnitur ngalami jaman sing kompetitif kaya akeh liyane, saengga ngupayakake golek cara kanggo nyuda biaya produksi, nambah kualitas, lsp. Minangka bagean saka program peningkatan produktivitas ing perusahaan manufaktur sing diarani (Perusahaan = TC) kita nindakake proyek kanggo ngoptimalake desain tata letak baris produksi ing lantai toko perusahaan iki kanggo ngatasi masalah saiki amarga tata letak sing ora efisien. Diputusake kanggo ngetrapake sawetara teknik pemodelan tata letak kanggo ngasilake tata letak sing paling optimal adhedhasar metode formal sing jarang digunakake ing praktik. Teknik pemodelan ingkang dipunginakaken inggih menika Graph Theory, Bloc Plan, CRAFT, Optimum Sequence lan Genetic Algorithm. Tata letak kasebut banjur dievaluasi lan dibandhingake nggunakake 3 kriteria yaiku Total Area, Aliran * Distrik lan Persentase Adjacency. Total Area nuduhake wilayah sing dikuwasani dening jalur produksi kanggo saben model sing dikembangake. Aliran * Dist ngitung jumlah produk aliran lan jarak antarane saben 2 fasilitas. Persentase Adjacency ngitung persentase fasilitas sing nyukupi syarat sing ana ing jejere.
Pamilihan tata letak sing paling apik uga ditindakake kanthi resmi
Dhéfinisi masalah tata letak pabrik yaiku nemokake susunan fasilitas fisik sing paling apik kanggo nyedhiyakake operasi sing efisien (Hassan lan Hogg, 1991). Tata letak mengaruhi biaya penanganan materi, wektu timbal lan throughput. Dadi mengaruhi produktivitas lan efisiensi sakabèhé tanduran. Miturut Tompkins lan White (1984) desain fasilitas wis ana ing sajarah sing kacathet lan pancen fasilitas kutha sing dirancang lan dibangun wis diterangake ing jaman kuna.
* Penulis sing cocog
sajarah Yunani lan Kakaisaran Romawi. Antarane 1st sing sinau masalah iki yaiku Armor lan Buffa et al. (1964). Sedikit kayane wis diterbitake ing taun 1950-an. Francis lan White (1974) minangka 1st sing ngumpulake lan nganyari riset awal ing wilayah iki. Riset mengko wis dianyari dening 2 pasinaon 1st dening Domschke lan Drexl (1985) lan liyane dening Francis et al. (1992). Hassan lan Hogg (1991) nglapurake studi ekstensif babagan jinis data sing dibutuhake ing masalah tata letak mesin. Data tata letak mesin dianggep minangka hirarki; gumantung carane rinci tata letak dirancang. Nalika tata letak sing dibutuhake mung kanggo nemokake susunan relatif mesin, data sing makili nomer mesin lan hubungan alirane cukup. Nanging, yen tata letak sing rinci dibutuhake, luwih akeh data dibutuhake. Ing nemokake data sawetara kangelan bisa njedhul utamané ing fasilitas Manufaktur anyar ngendi data durung kasedhiya. Nalika tata letak dikembangake kanggo fasilitas modern lan otomatis, data sing dibutuhake ora bisa dipikolehi saka data historis utawa saka fasilitas sing padha amarga bisa uga ora ana. Pemodelan matematika wis disaranake minangka cara kanggo entuk solusi optimal kanggo masalah tata letak fasilitas. Wiwit model matématika pisanan dikembangaké déning Koopmans lan Beckmann (1) minangka masalah tugas kuadrat, kapentingan ing wilayah wis kepincut wutah owahan. Iki mbukak lapangan anyar lan menarik kanggo peneliti. Nalika nggoleki solusi kanggo masalah tata letak fasilitas, peneliti miwiti ngembangake model matematika. Houshyar lan White (1957) nliti masalah tata letak minangka an
Ijo lan
2. PENDEKATAN MODEL
Model dikategorikake gumantung saka sifat, asumsi lan tujuane. Pendekatan Perencanaan Tata Letak Sistematis generik 1, sing dikembangake dening Muthor (1955), isih dadi skema sing migunani utamane yen didhukung dening pendekatan liyane lan dibantu dening komputer. Pendekatan konstruksi, Hassan lan Hogg (1991) contone, mbangun tata letak saka ngeruk nalika Metode Improvement, Bozer, Meller and Erlebacher (1994) contone, nyoba ngowahi tata letak sing wis ana kanggo asil sing luwih apik. Cara ngoptimalake lan uga heuristik kanggo tata letak kanthi didokumentasikake kanthi apik dening Heragu (2007).
Macem-macem teknik pemodelan sing digunakake ing karya iki yaiku Teori Grafik, CRAFT, Urutan Optimum, BLOCPLAN lan Algoritma Genetik. Diterangake ing ngisor iki minangka paramèter sing dibutuhake saben algoritma kanggo nggawe model sing padha.
Teori Grafik
Teori grafik (Foulds lan Robinson, 1976; Giffin et al., 1984; Kim lan Kim, 1985; lan Leung, 1992) ditrapake
Makalah iki nggunakake 2 macem-macem pendekatan kanggo model studi kasus. Pendekatan 1st yaiku
Nggunakake CRAFT
CRAFT (Computerized Relative Allocation of Facilities Technique) nggunakake ijol-ijolan sing wicaksana pasangan kanggo ngembangake tata letak (Buffa et al., 1964; Hicks and Lowan, 1976). CRAFT ora nliti kabeh ijol-ijolan sing wicaksana pasangan sadurunge nggawe tata letak sing luwih apik. Data input kalebu dimensi bangunan lan fasilitas, aliran materi utawa frekuensi lelungan antarane pasangan fasilitas lan biaya saben unit beban saben unit jarak. Produk aliran (f) lan jarak (d) nyedhiyakake biaya kanggo mindhah bahan antarane 2 fasilitas. Pengurangan biaya kasebut banjur diitung adhedhasar kontribusi biaya penanganan bahan pra lan pasca ijol-ijolan.
Urutan paling optimal
Cara solusi diwiwiti kanthi tata letak urutan sing sewenang-wenang lan nyoba nambah kanthi ngganti 2 departemen ing urutan kasebut (Heragu, 1997). Ing saben langkah, cara ngetung aliran * owah-owahan jarak kanggo kabeh saklar 2 departemen lan milih pasangan sing paling efektif. 2 departemen diowahi lan metode kasebut diulang. Proses mandheg nalika ora ana switch nyebabake biaya suda. Input sing dibutuhake kanggo ngasilake tata letak nggunakake Urutan Optimal utamane dimensi bangunan lan fasilitas, aliran materi utawa frekuensi lelungan antarane pasangan fasilitas lan biaya saben unit beban saben unit jarak.
Nggunakake BLOCPLAN
BLOCPLAN minangka program interaktif sing digunakake kanggo ngembangake lan nambah tata letak siji lan bertingkat (Ijo lan
ngasilake sawetara tata letak blok lan ukuran fitness. Pangguna bisa milih solusi relatif adhedhasar kahanan.
Algoritma Genetik
Ana akeh cara kanggo ngrumusake masalah Layout fasilitas liwat algoritma genetika (GA).Banerjee, Zhou, lan Montreuil (1997) Applied GA kanggo tata letak sel. Pendekatan kasebut banjur digunakake dening akeh penulis kalebu Tam lan Chan (1) sing digunakake kanggo ngatasi masalah tata letak area sing ora padha karo kendala geometris. Algoritma GA sing digunakake ing karya iki dikembangake dening Shayan lan Chittilappilli (1982) adhedhasar slicing tree structures (STC). Iki menehi kode tata letak calon sing disusun wit dadi struktur khusus kromosom 1995 dimensi sing nuduhake lokasi relatif saben fasilitas ing wit sing diiris. Skema khusus kasedhiya kanggo ngapusi kromosom ing operasi GA (Tam lan Li, 2004). A anyar "kloning" operasi uga ngenalaken ing Shayan lan
3. EKSPERIMENTASI VIA STUDI KASUS
Kanggo nguji kinerja metode sing diterangake sadurunge, kabeh mau ditrapake kanggo skenario kasus nyata ing manufaktur furnitur. Perusahaan ngasilake 9 macem-macem gaya Kursi, 2- Seater lan
Saben produk dadi liwat 11 operasi kang diwiwiti ing Facility 1 - Cutting Area lan pungkasan ing Facility 11- Bolt munggah Area. Saben rakitan pungkasan bisa dipérang dadi subassemblies kanthi jeneng sing padha. Subassemblies iki ketemu ing Bolt
Amarga iki, ora ana aliran bahan sing berurutan, nyebabake karya sing ditindakake. Interaksi antarane fasilitas bisa ditemtokake nggunakake ukuran subyektif uga obyektif. Input utama sing dibutuhake kanggo diagram alur yaiku panjaluk, jumlah bahan sing diprodhuksi lan jumlah materi sing mili ing antarane saben mesin. Aliran materi diitung adhedhasar jumlah aliran materi sing lelungan saben 10 sasi * Unit ukuran sing ditampilake ing Gambar 2. Gambar 3 nuduhake area saben departemen sing digunakake ing studi kasus. Gambar 4 nuduhake tata letak Studi Kasus saiki.
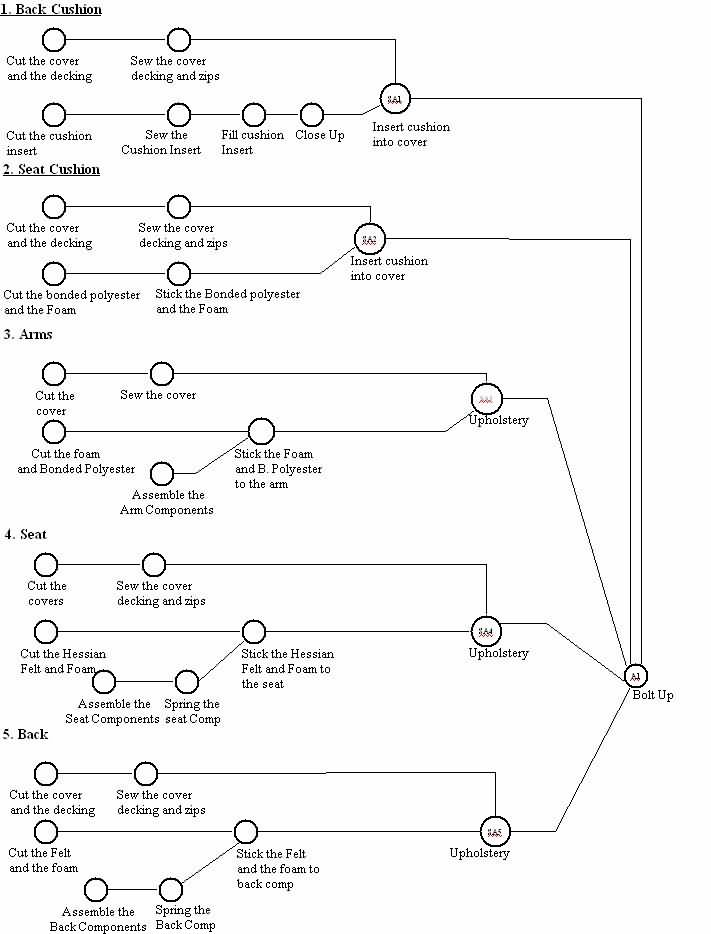
Gambar 1 Bagan perakitan kanggo studi kasus
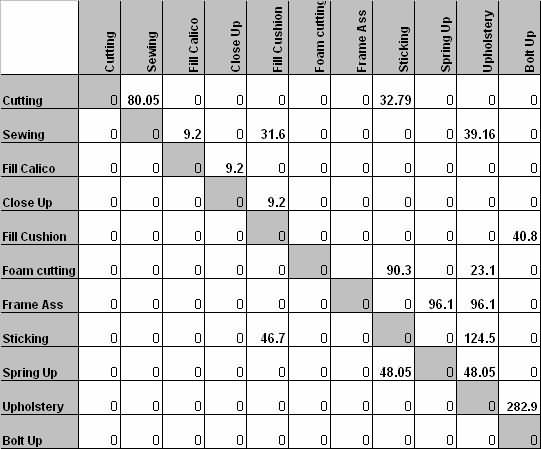
Gambar 2 Alur materi pasinaon kasus.
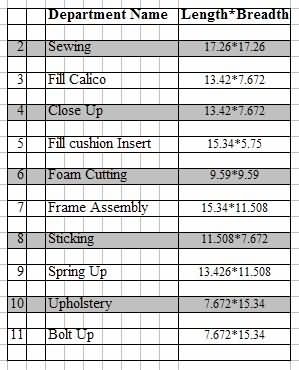
Gambar 3 Nomer sing cocog karo departemen
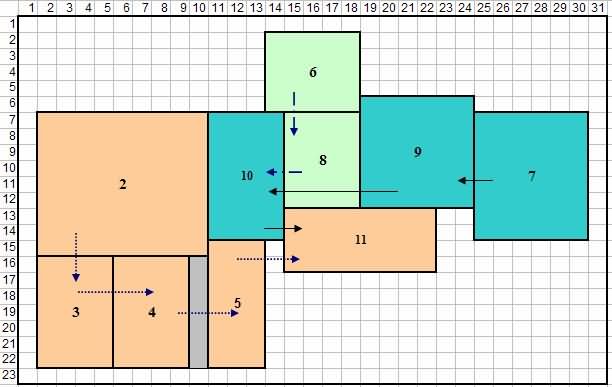
Gambar 4 Tata letak saiki perusahaan mebel lan dimensi saben departemen sing digunakake ing modeling studi kasus
4. APLIKASI PENDEKATAN MODEL
Ing kene macem-macem pendekatan model sing dibahas ing bagean 2 ditrapake kanggo studi kasus kanggo ngasilake tata letak alternatif kanggo mbandhingake.
4.1 Nggunakake Teori Grafik
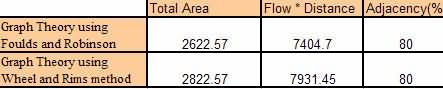
Tabel 1 nuduhake perbandingan asil nggunakake 2 pendekatan Teori Grafik sing beda yaiku metode Foulds lan Robinsons lan metode Wheels and Rims. Tabel 1 kanthi jelas nuduhake yen metode Foulds lan Robinsons luwih apik tinimbang asil 2. Asil metode Foulds lan Robinsons diterangake kanthi rinci ing Gambar
Tabel 1: Tabel sing nuduhake perbandingan 2 metode teori grafik sing digunakake.
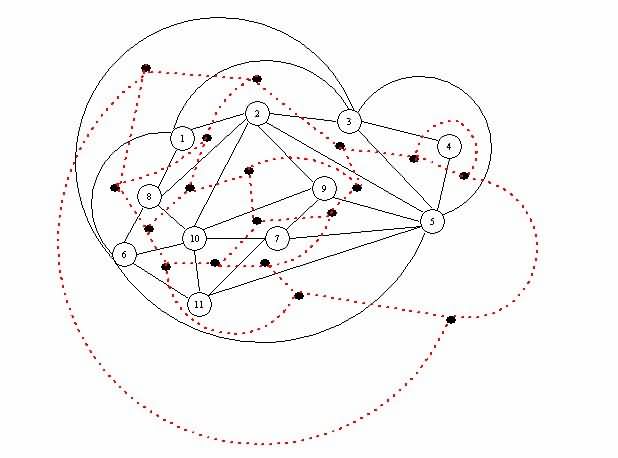
Gambar 5 Grafik adjacency asil studi kasus nggunakake metode Foulds lan Robinson.
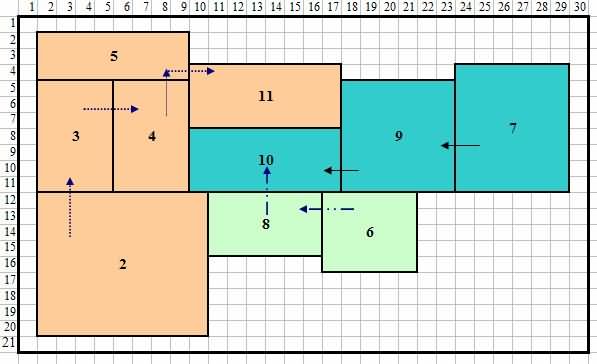
Gambar 6 Tata letak sing luwih apik sawise nggunakake teori grafik (metode Foulds lan Robinsons)
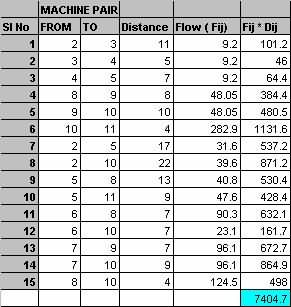
Gambar 7 Alur * Bagan evaluasi jarak kanggo studi kasus nggunakake teori grafik (metode Folds lan Robinsons)
4.2 Nggunakake CRAFT
Data input kanggo CRAFT dilebokake lan biaya wiwitan kanggo tata letak saiki diwilang kaping 1. Biaya iki bisa suda nggunakake pasangan wicaksana comparison minangka ditampilake ing Figures 8,9.
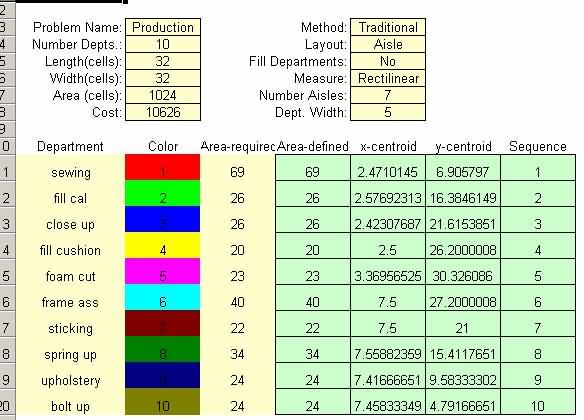
Figure 8 Biaya dhisikan kanggo tata letak saiki nggunakake CRAFT
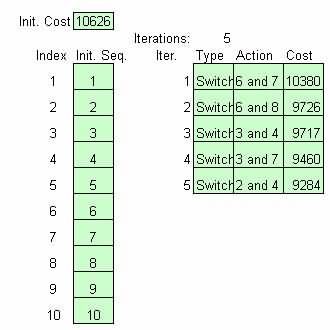
Figure 9 Step by step exchange dening CRAFT
Asil sing dipikolehi dening CRAFT ditampilake ing Tabel 2. Adhedhasar petungan ing ndhuwur bisa digambar tata letak anyar lan apik sing ditampilake ing Gambar 10
Tabel 2: Tabel sing nuduhake asil

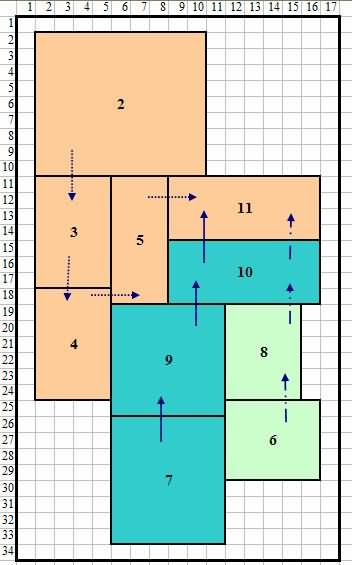
Gambar 10 Ngapikake tata letak digawe dening CRAFT
4.3 Algoritma urutan paling optimal
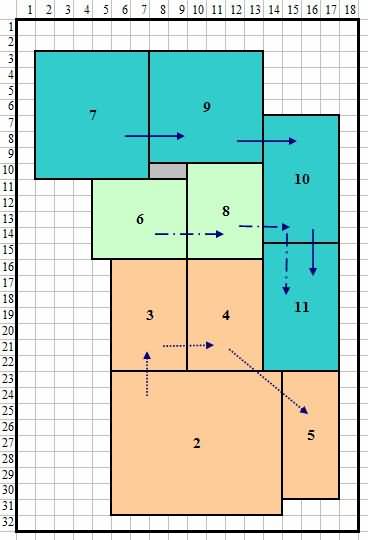
Data input padha kanggo CRAFT kajaba sing nderek pesawat beda saka comparison wicaksana pasangan. Tabel 3 nuduhake asil sing digambar saka tata letak sing luwih apik. Gambar 11 nuduhake tata letak sing luwih apik nggunakake Urutan Optimum.
Tabel 3 Tabel nuduhake asil nggunakake CRAFT

4.4 Nggunakake BLOCPLAN
Bagan matriks aliran diowahi dadi grafik REL kaya sing ditampilake ing Gambar 12 kanthi paramèter ing ngisor iki:

Gambar 12 Bagan REL kanggo studi kasus

Tabel 4 nuduhake asil nggunakake macem-macem pendekatan. Kaya sing katon ing BLOCPLAN nggunakake telusuran otomatis nuduhake asil sing luwih apik tinimbang nggunakake Algoritma Konstruksi.
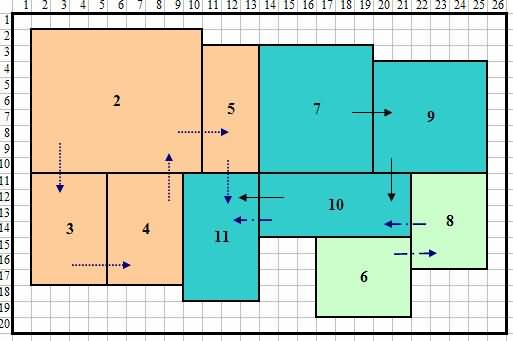
Gambar 13 Telusuran otomatis tata letak sing luwih apik

Tabel 4 Ukuran kanggo tata letak BLOCPLAN
4.5 Nggunakake Algoritma Genetik
Solusi paling apik ditemokaké dening algoritma ditampilake ing Figure 14. Iki banjur diowahi kanggo tata letak ing Figure 15 kanggo bandingaken umum karo model liyane.

Gambar 14 Tata letak sing dikembangake kanthi algoritma genetika
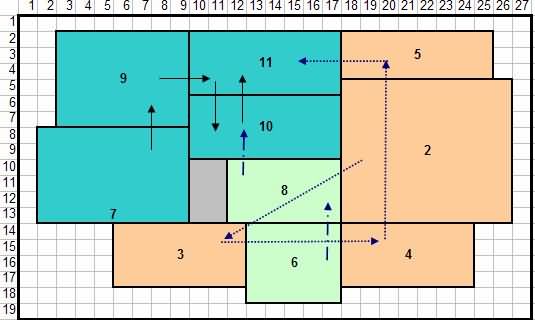
Gambar 15 Konversi tata letak ing Gambar 14
Tabel 5 nuduhake asil nggunakake Algoritma Genetik.

Tabel 5 Tabel sing nuduhake asil nggunakake algoritma genetika
5. BANDINGAN ASILE EKSPERIMENTASI DENING AHP
Tabel 6 ngringkes asil sing dipikolehi saka kabeh teknik pemodelan lawan Tata Letak Saiki kanggo mbandhingake. Bagean tata letak sing paling apik bakal ditindakake adhedhasar 3 faktor yaiku Total Area (Minimze), Aliran * Jarak (Maximize) lan Persentase Adjacency (Maximize). Tujuan utama yaiku nyuda WIP lan ngatur aliran materi sing sistematis. Akibaté aliran * matriks jarak minangka parameter sing paling penting.
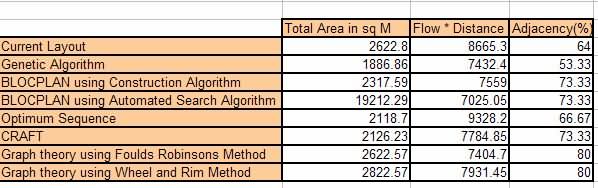
Tabel 6 Ringkesan asil nggunakake kabeh Techniques modeling versus asil saka tata letak saiki
Tabel 7 nuduhake rangking campuran saka tata letak alternatif adhedhasar macem-macem faktor. Contone Layout 1 wis pangkat miskin ing Area lan F * D nalika iku paling apik ing Adjacency. Kombinasi ndadekake angel kanggo milih siji saka liyane. Kita nggusah nggunakake technique formal, AHP, dipun ginakaken dening piranti lunak Expert Choice.
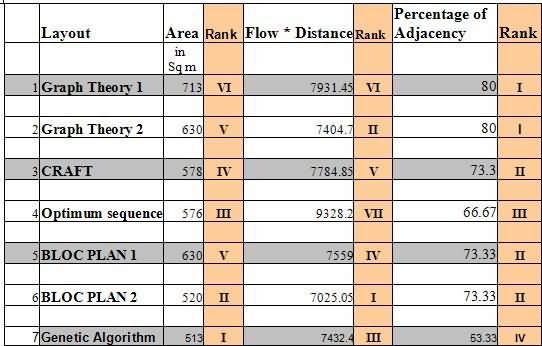
Tabel 7 Rangking saka macem-macem alternatif babagan tujuan
AHP mbandhingake pentinge relatif saben pasangan bocah karo wong tuwa. Sawise perbandingan pasangan rampung, pendekatan sintesis asil nggunakake sawetara model matematika kanggo nemtokake peringkat sakabèhé. Gambar 16 nuduhake peringkat asil sing diraih saka kabeh algoritma kanthi tujuan solusi pilihan sing paling apik.
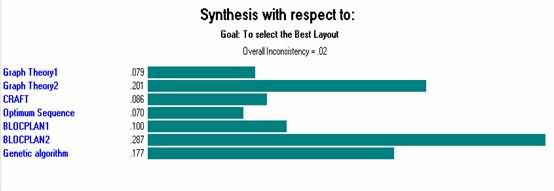
Gambar 16 Sintesis babagan tujuan
Solusi paling apik digayuh kanthi BLOCPLAN (Telusuri Otomatis) banjur Teori Grafik nggunakake Metode Foulds lan Robinsons, banjur Algoritma Genetik. Solusi liyane luwih elek. Elinga, amarga peringkat subyektifitas sing ana ora minangka indikasi mutlak kanggo pilihan sing luwih apik, nanging minangka rekomendasi sing bisa ditindakake pangguna supaya cocog karo kabutuhan.
Kita ngusulake tata letak sing digawe nggunakake BLOCPLAN nggunakake Panelusuran Otomatis dadi solusi sing dipilih. Nalika iki diputus, analisis sensitivitas ditindakake kanggo mesthekake yen pilihan kasebut kuat. Yen wektu ngidini iki kudu rampung kanggo alternatif cedhak liyane sadurunge pilihan digawe.
6. PANUTUP
Tujuan ing makalah iki yaiku nggunakake macem-macem teknik pemodelan kanggo milih tata letak sing paling apik kanggo perusahaan furnitur. Tata letak paling apik digawe dening BLOCPLAN nggunakake Panelusuran Otomatis kaya ing Gambar 17.
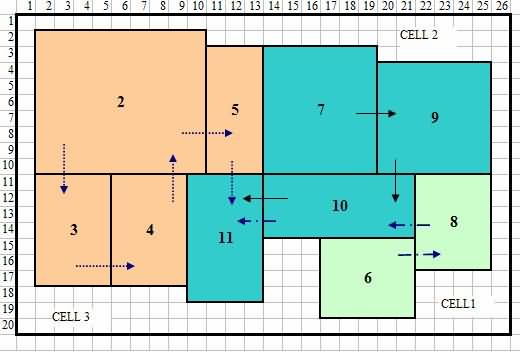
Gambar 17 Tata letak paling apik nggunakake pendekatan modeling
Tabel 9 nuduhake dandan saka solusi ngajokaken liwat tata letak saiki. Elinga yen tata letak nuduhake blok lan lokasi sing relatif. Watesan praktis kudu ditrapake kanggo cocog karo kabeh kabutuhan. Banjur rincian liyane saben blok bisa direncanakake, yen perlu kanthi cara sing padha.

Tabel 9: Dandan liwat tata letak saiki nggunakake Techniques modeling
Asil kasebut cukup marem kanggo perusahaan, sing ora duwe kawruh babagan pendekatan ilmiah.



